トライボロジー(摩擦・摩耗)の基礎
トライボロジーの基礎を解説します。
まず、1.固体表面の接触・構造について触れ、2.摩擦、3.摩耗と解説します。摩耗では、古くから提唱されているいくつかの摩耗形態について述べた後、現在最も受け入れられている笹田先生の凝着摩耗の移着成長モデルについて解説します。
1.固体表面の接触・構造
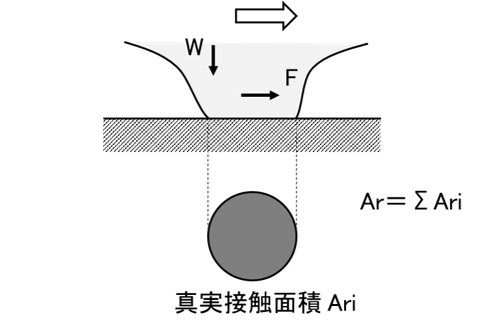
固体表面には、粗さやうねりが存在するため、平面同士の接触であっても、微視的にみると図1に示すような突起同士の接触になります。この突起同士での接触部のことを真実接触部と呼び、その面積の和を真実接触面積と呼びます。真実接触面積は、見かけの接触面積の1/10~1/1000程度とかなり小さく、見かけの接触面積(A0)よりも真実接触面積(Ar)が摩擦や摩耗には重要です。真実接触面積の考え方は凝着説に基づく摩擦理論や凝着摩耗の基礎となります。
実際の平面同士の接触の模式図
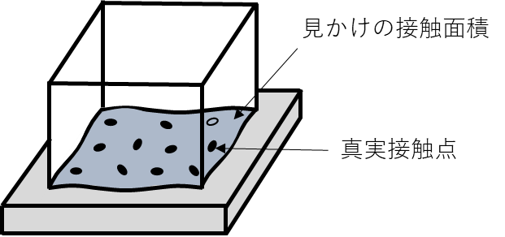
例えば金属の接触において、真実接触面積は見かけの接触面積に比べ極端に小さいので個々の真実接触点が支える荷重は弾性接触域を超え、ほぼその材料の塑性流動圧力pmに達して塑性変形していると考えられます。この場合、以下の関係式が成り立ち、真実接触面積が荷重に比例し、材料の塑性流動圧力に反比例することが分かります。
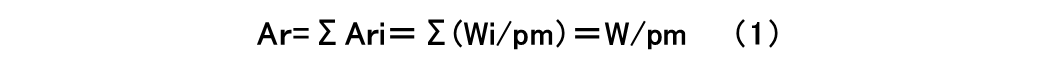
なお、ここでは全ての真実接触点が塑性接触しているとしていますが、塑性接触と弾性接触の比率を把握するためには塑性指数Ψという概念が必要となります。塑性指数は材料のヤング率、硬度に加え、接触表面の合成粗さや突起の曲率半径を加味したパラメーターで、Ψが0.6以上でほぼ塑性接触、それ以下では弾性接触と塑性接触の両方が存在する接触状態と言われています。
表面性状を評価するパラメータ
表面性状(形状、粗さ)を評価するパラメータは、JIS B 0601: 2013(輪郭曲線方式:二次元断面)およびJIS B 0681-3: 2019 (三次元)に規定されています。下表では、よく利用されているJIS B 0601: 2013既定の表面性状パラメータについて紹介します。
パラメータの計算元となる曲線には、二次元断面で得られる断面曲線、断面曲線から長波長成分をカットした粗さ曲線、短波長成分をカットしたうねり曲線があり、注目する項目によって使い分けますが、粗さ曲線で議論することが最も多いです。
粗さ曲線を表すパラメータとしては、算術平均高さRa、二乗平均平方根高さRq(あるいはRMS)、最大高さRzなどがよく用いられています。また、最近は山谷の形状も加味したスキューネスRskやクルトシスRkuなども用いられています。
表 JIS B0601 2013既定の表面性状パラメータ一覧
| 評価曲線 | 断面曲線 | 粗さ曲線 | うねり曲線 | |
|---|---|---|---|---|
| 山及び谷の高さ パラメータ | 最大山高さ | Pp | Rp | Wp |
| 最大谷深さ | Pv | Rv | Wv | |
| 最大高さ | Pz | Rz | Wz | |
| 要素の平均高さ | Pc | Rc | Wc | |
| 最大断面高さ | Pt | Rt | Wt | |
| 高さ方向の パラメータ | 算術平均高さ | Pa | Ra | Wa |
| 二乗平均平方根高さ | Pq | Rq | Wq | |
| スキューネス | Psk | Rsk | Wsk | |
| クルトシス | Pku | Rku | Wku | |
| 横方向の パラメータ | 平均長さ | PSm | RSm | WSm |
| ピークカウント数 | PPc | RPc | WPc | |
| 複合パラメータ | 二乗平均平方根傾斜 | PΔq | RΔq | WΔq |
| 負荷長さ率 | Pmr(c) | Rmr(c) | Wmr(c) | |
| 切断レベル差 | Pδc | Rδc | Wδc | |
| 相対負荷長さ率 | Rmr | Rmr | Wmr |
表面をより詳細に評価するためには、白色干渉顕微鏡、共焦点顕微鏡などを用いて、三次元の表面性状を解析します。
また、走査型プローブ顕微鏡(Scaning Probe Micoroscope; SPM)を用いてナノレベルの表面性状を評価することもできます。
固体表面層の構造
固体の表面層は内部とは全く異なる構造をしているといわれています。金属の表面は機械加工などで仕上げられていることが多く、表層にはせん断による加工変質層が存在し、さらにその上には酸化膜の層、さらには主に有機物からなるコンタミ層が形成されています。
鋼表層断面の模式図
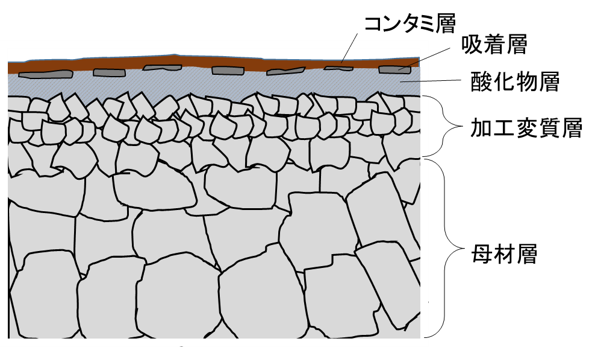
加工変質層は内部より微細な結晶粒からなるとされていることが多いですが、冷間での機械加工で仕上げられたのであれば、加工変質層の結晶粒は表層でのせん断のため扁平した結晶粒となっていることが多いです。機械加工後に熱処理などが行われた場合、再結晶などが生じて等方な微細結晶粒となることもあります。
いずれの場合も、これらの加工変質層は内部よりは硬度が高くなっていると考えることができます。
加工変質層の上には通常酸化膜の層が形成されています。機械加工で生まれた新生面は化学的な活性(表面エネルギー)が高いため、大気中では酸素や水分の吸着により酸化膜が生じます。冷間での酸化膜は一般にFe2O3、Fe3O4でnmオーダーと言われています。
表層の構造を把握するには、着目する部位に応じて、表面および断面からの光学顕微鏡観察、透過電子顕微鏡観察、走査電子顕微鏡観察など各種表面分析機器による観察が行われています。また、表層の硬度を確認する方法としては、表面および断面からの各種硬度測定、さらには局所的なナノ硬度を測定するナノインデンテーション測定などにより把握することができます。
2.摩擦
摩擦については、アモントン-クーロン(Amonton-Coulomb)の法則が知られています。
- 摩擦力は摩擦面に作用する垂直荷重に比例し、見かけの接触面積にはよらない
- 摩擦力は滑り速度に無関係である
- 静止摩擦力は動摩擦力よりも大きい
アモントン-クーロンの法則は、経験則であり、通常の実用摩擦条件ではほぼ成り立ちますが、表面状態や摩擦条件によっては成り立たない場合もあります。
アモントン-クーロンの法則より、摩擦力は荷重に比例しますので、その比例定数を摩擦係数(friction coeficientまたはcoefficient of friction) μと定義され、(2)式のように表わされます。
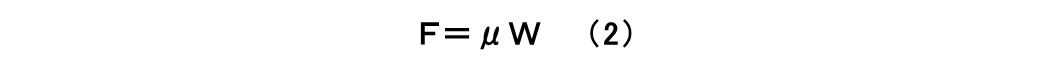
この摩擦係数μは摩擦状態を評価する値として広く用いられていますが、材料固有の物性値でなく、材料の組み合わせ、摩擦条件などによって変化する値です。
摩擦係数の物理的意義を理解する上で重要なのが摩擦力の起源です。摩擦力の起源としては、凝着説と掘起こし説があります。
摩擦力の起源
凝着説
凝着説では、真実接触点で2面間の凝着が生じ、その凝着部をせん断するのに必要な力の総和が摩擦力とされています。
ある真実接触点で発生する摩擦力は、その真実接触点の面積Ariとせん断強さsの積で表され、真実接触面積の和Ar=ΣAriとすると、凝着による摩擦力は
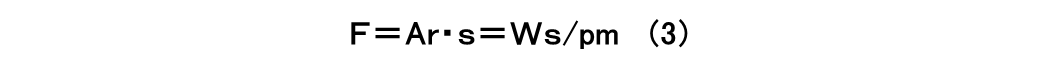
となり、また前述のようにAr=W/pmですので、
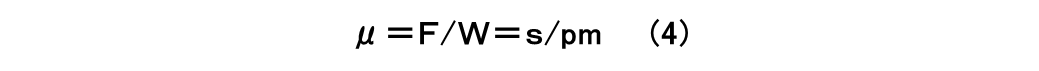
となります。ここで、pmは先述の塑性流動圧力です。金属の場合、せん断強さsは降伏応力の0.5倍程度とされており、また塑性流動圧力pmは降伏応力の約2.8倍とされています。したがって、金属の場合の摩擦係数は約0.18となります。そこに、後述の掘起こし項を考慮しても摩擦係数は0.18~0.3程度が妥当と言われています。ただ、著しい焼き付きが生じた場合など、1を超える大きな値をとることもあります。
真実接触点の模式図
掘起こし説
次に、摩擦における掘起こし項について考えます。下図のように半球の突起が相手材の表面から内部に食い込みながら滑っている状況を考えます。ある突起iが相手材を掘り起こす力は、掘り起こし面積(投影面積)Aiと相手材の塑性流動圧力pmの積となり、掘起こし面積の和Ah=ΣAiとすると、掘起こしによる摩擦力は

となり、摩擦力は凝着項と掘起こし項の和として表され、

ただし、金属同士の摩擦においては、突起の曲率は非常に小さいため、Arに比べAhは小さくなり掘起こし項は無視できるとされています。
掘起こし摩擦の模式図

3.摩耗
摩耗は産業界におけるトライボロジー課題の中で最も頻繁に生じる現象の一つです。機械の寿命や故障の原因が、摩耗に起因することもよくあります。摩耗は摩擦によって物体表面に起こる材料損失のことです。摩擦と摩耗は表裏一体の関係にありますが、それぞれは独立した現象で、摩耗量が多いからと言って、必ずしも摩擦係数が高いということはありません。
摩耗の形態は、古くから凝着摩耗、アブレシブ摩耗、腐食摩耗、疲労摩耗の4つに大別されます。これ以外にも幾つか摩耗形態が提唱されていますが、この4つが最も代表的な摩耗形態です。
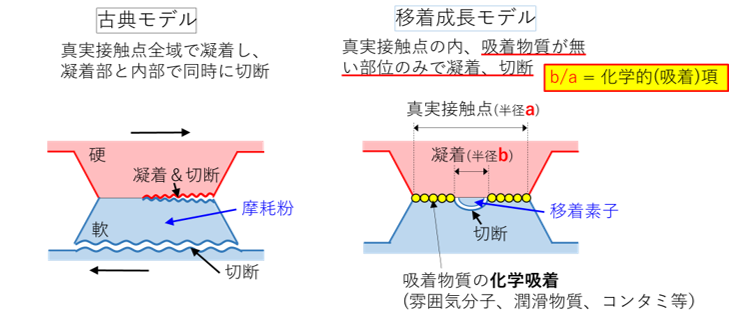
凝着摩耗(古典モデル)
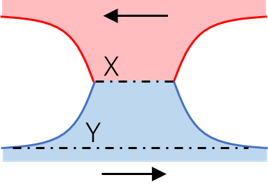
まず凝着摩耗は、真実接触部で材料同士が凝着し、それがせん断させるときにその一部が材料内部でちぎれて、摩耗粉として発生する形態の摩耗です。この凝着摩耗が摩耗の基本的なメカニズムとして現在受け入れられています。ただ、ここで示すようなシンプルな機構ではありません。この点については後述します。
この(古典)モデルでは、摩耗粉が生じるにはX-XとY-Yが同時にせん断破壊される必要があり、不自然です。また、この機構では軟らかい材料のみが摩耗しますが、実際は硬い方の材料も摩耗します。また、摩耗粉サイズについても、このモデルでは粗さの突起サイズ、つまりサブミクロンオーダーとなりますが、実際はシビアな摩耗ではもう一桁大きく数ミクロンオーダーですし、マイルドな摩耗ではもう一桁小さく数十ナノ程度がメインとなることが多く、実際と合いません。
アブレシブ摩耗
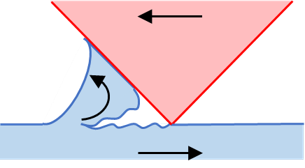
次に、アブレシブ摩耗は、粗さの突起部が相手側の材料の接触部位を排除する、つまり削ることによって摩耗するというモードです。アブレシブとは研磨、研削と言った意味です。
アブレシブ摩耗は、摩擦のご説明のところで出てきた「掘起こし項」による摩耗です。一般的な摩擦では凝着項が支配的で、この掘起こし項の影響はかなり小さく無視できるケースも多いのですが、そんな中でも掘起こし項の影響が比較的大きい場合に、「この摩耗はアブレシブ摩耗」と表現します。ただ、研磨紙で削ったり、砥粒で研磨するような場合は、つまり例えば金属とセラミックスの摩擦など、凝着が起こり難い場合は、アブレシブ摩耗が主体となります。
疲労摩耗
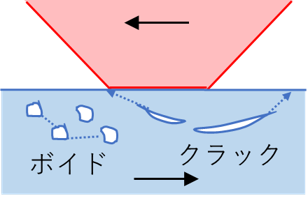
次に疲労摩耗ですが、摩耗の原因とするのは無理があります。疲労は起こりますし、それによって表面の損傷は起きます。例えば、ピッチングなどの剥離損傷がそれに当たります。
腐食摩耗
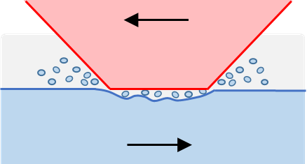
さらに、腐食摩耗というのがありますが、確かに腐食環境では摩耗が良く進み、腐食が主因ととらえることのできることは多いです。ただ、腐食環境であっても摩耗の起点は凝着部や掘起こし部で、その時に腐食によって脱離する摩耗粉が促進されるから腐食摩耗と呼ばれたりします。
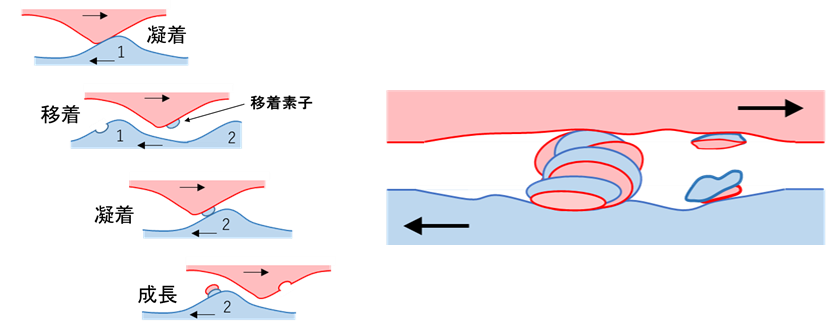
摩耗の移着成長モデル
前述のように摩耗のメインは凝着摩耗ですが、古典モデルは矛盾も多いです。それに対して現在もっとも受け入れられているモデルは、摩耗の移着成長モデルというもので、元東工大の笹田先生により体系的に提唱されました。
移着成長モデルはこの図に示すように、ある粗さの突起部で上下が接触して真実接触点を形成して凝着が生じます。そして、移動してその部位での接触が破断する際に、一方の材料が他方に移着します。この相手面に移着した粒子は「移着素子」と呼ばれます。古典モデルではこの移着素子そのものが摩耗粉と表現されていましたが、そうではなく、凝着面は接着したまま、下側の材料の内部でせん断破壊が生じ、上側の材料に移着します。
次に、移着下側の上側の突起部は別の下側の突起と接触し、そこで新たな凝着を生じます。すると今度は、上側の材料の内部でせん断破壊が生じ、下側の材料に移着します。必ずしも交互に起こるわけではないのですが、移着は繰り返され、図のように、ある大きさになると左右方向のモーメントにより摩耗粉として脱離します。移着は2面の軟らかい方の材料から生じやすく、相手材に移着することが多いです。但し、その逆もあります。これは、表面凹凸形状および接触は規則的ではないため、真実接触部は上下必ずしも対称とは限らないからです。硬い方に内部欠陥があったり、形状が軟らかい方のそれに比べて高荷重に耐えられない場合、せん断が固い方の材料で生じて、その移着素子が軟らかい方に移着することもあります。
このモデルでは、両方の材料が共に摩耗する現象も説明でき、実測された摩耗粉に両方の材料が含まれていることも説明できます。さらに、摩耗粉サイズがシビアな摩耗では真実接触点のサイズ、つまり粗さの突起先端部のサイズより1オーダー大きな粒子や、逆に1オーダー小さな粒子となることも説明できます。
凝着摩耗の移着成長モデルの模式図
移着成長モデルについて、もう少し詳しく説明します。古典モデルによる凝着摩耗では、真実接触点で接触した部位全体で凝着が起き、軟らかい材料の内部で破断が起きると同時に、凝着した接触界面も同時に破断するという不自然なモデルです。
一方、右側の移着成長モデルでは、移着が起こる際、真実接触点の全面、ここでは、接触部が円として半径a、全体で移着が起こるのではなく、そのうちの一部、ここでは半径bとしていますが、この部位のみで移着が起こります。真実接触点の両表面には接触前には、コンタミの有機物や吸着雰囲気で覆われています。その後、接触とせん断で、それらの汚れは脱落し、一部で金属面が露出して、直接メタルとメタルが接触します。この直接接触している半径bの部位で金属が凝着して移着が生じます。つまり、移着は真実接触点のなかでも介在する吸着物が無くなった部位のみで生じます。繰り返しの摩擦の中で、雰囲気の吸着が深くかかわった現象です。
吸着物質が強固に吸着していれば、bは小さくなり、つまり、移着は起こりにくくなり、摩耗の程度小さくなります。このように、移着成長モデルではb/aと言う形で、気体や油の吸着と言った潤滑の影響、つまり、化学的な項を取り入れています。
凝着摩耗の模式図
繰り返し摩耗の摩耗量の時間的変化
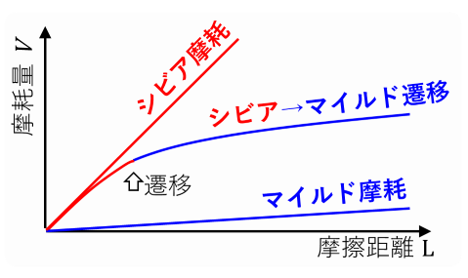
繰り返し摩擦における摩耗量の時間的変化を描くと図のようになります。
一般的な摩耗、つまりこれまで説明したような移着成長を繰り返す凝着摩耗では、摩耗条件によって、大きく分けて2つの激しさの摩耗が現れます。ひとつは、摩耗速度が速い、つまり図の摩耗曲線の傾きが大きい摩耗で、シビア摩耗とよばれます。もう一つは、摩耗速度が遅い、つまり傾きが小さい摩耗で、マイルド摩耗と呼ばれます。
摩耗進行曲線
その摩耗曲線を数式的に表現するものとして、「摩耗式」という経験式があります。この式は、摩耗量Vは面圧Pと摩擦距離Lに比例し、材料の硬さPmに反比例するというもので、感覚的には受け入れやすいものとなっています。この時の比例係数が摩耗係数Zです。移着成長モデルではZはb/aの3乗に比例します。式の導出は笹田先生の書著「摩耗」をご参照ください。

シビア摩耗とマイルド摩耗
シビア摩耗ではb/aは大体1/2~1/5程度となり、マイルド摩耗では1/20~1/50と、ワンオーダー位変わります。それの伴って摩耗係数はシビア摩耗で10-2~10-3となり、マイルド摩耗ではそれよりスリーオーダーほど低くなります。また、摩耗粉サイズを比較すると、シビア摩耗では、凝着しやすい環境ですので、移着が成長し、数ミクロンもの大きく成長した摩耗粉となり、一方のマイルド摩耗では、移着が起きにくい環境ですので、移着素子の成長も少なくサブミクロン以下の小さな摩耗粉を形成します。
マイルド摩耗では真実接触点のかなり広いエリアで気体分子が界面に介在しているためb/aが小さくなり、その結果摩耗量が小さくなっています。それに対し、シビア摩耗では気体分子があまり界面に介在していないので凝着エリアb/aが大きくなり摩耗量も大きくなっています。
移着成長モデルによる摩耗式とその概要

シビア・マイルド摩耗遷移
摩耗進行曲線の図において途中で傾きが変わってる摩耗挙動は、最初は気体分子の吸着が少なくシビア摩耗であったものが、ある段階で気体分子が吸着しはじめ、b/aが小さくなりマイルド摩耗に遷移する現象です。この現象を摩耗のシビア・マイルド摩耗遷移と呼び、多くの繰返し摩擦で現れる現象です。
シビア摩耗になるかマイルド摩耗に移行できるかを決めるb/aは、平均自由時間t、その間の気体の化学吸着を支配する因子Tや活性化エネルギーなどの関数となりますが定量化されていません。平均自由時間とは、ある一つの真実接触点が一度相手材と接触して吸着物がせん断されて脱離しても、その突起が次にまた相手材の別の突起と接触するまでの時間です。
2面間の相互作用
化学吸着の吸着活性には、吸着される固体側の影響も大きいです。
直接接触部での両金属の相互作用力も移着成長に大きく影響します。一般に、両金属の相互溶解度が高ければ移着成長しやすく、低ければ移着は成長しにくいです。各金属の相互溶解度が低いほど移着成長が進みにくく、摩耗量は少なくなる傾向にあります。*1
*1 純金属の相互溶解度 、「トライボロジー入門」山本著、幸書房

