破壊限界ひずみ評価技術

破壊限界ひずみ評価技術とは

材料の数値シミュレーション(CAE: Computer Aided Engineering)において破断現象を取り扱う際、その材料がどこまで変形すると破断するという閾値、すなわち、「破断限界ひずみ」を設定する必要があります。そして、破断限界ひずみの値は、その材料に生じている応力の多軸度合いを表す指標である「応力三軸度」に依存すると言われています。破断限界ひずみの応力三軸度依存性を評価し、それをCAEの条件に取り込むことで、破断現象のシミュレーション精度を向上させることが期待できます。

破壊限界ひずみ評価技術の特徴

評価に必要な以下のプロセス全てに対応が可能です。

試験計画の立案
試験片の形状の決定と作製
引張試験機等による試験片への多軸応力付与
破断限界ひずみの評価
デジタル画像相関法(DIC)を活用した測定も可能
数値シミュレーション(CAE)を用いた応力三軸度の評価

破壊限界ひずみ評価技術の適用分野

自動車分野
板のプレス成形・衝突解析における材料の破断シミュレーション
エンジニアリング分野
地震などにより発生する複雑な応力状態における材料の破断シミュレーション

破壊限界ひずみ評価技術の原理

破断限界ひずみは破断までの変形量、応力三軸度は発生している応力の多軸度合いを表す指標です。応力三軸度はηで示され以下の式(1)、(2)、(3)で定義されます。

　 η=σ_m/σ …(1)
　 σ_m=1/3(σ₁+σ₂+σ₃ ) …(2)
　 σ ̅=√(1/2{(σ₁−σ₂)²+(σ₂−σ₃ )²+(σ₃−σ₁)²}) …(3)

ここで、
σ_m :平均垂直応力　　
σ ̅:ミーゼスの相当応力　　
σ_{1, 2, 3}:主応力　
です。

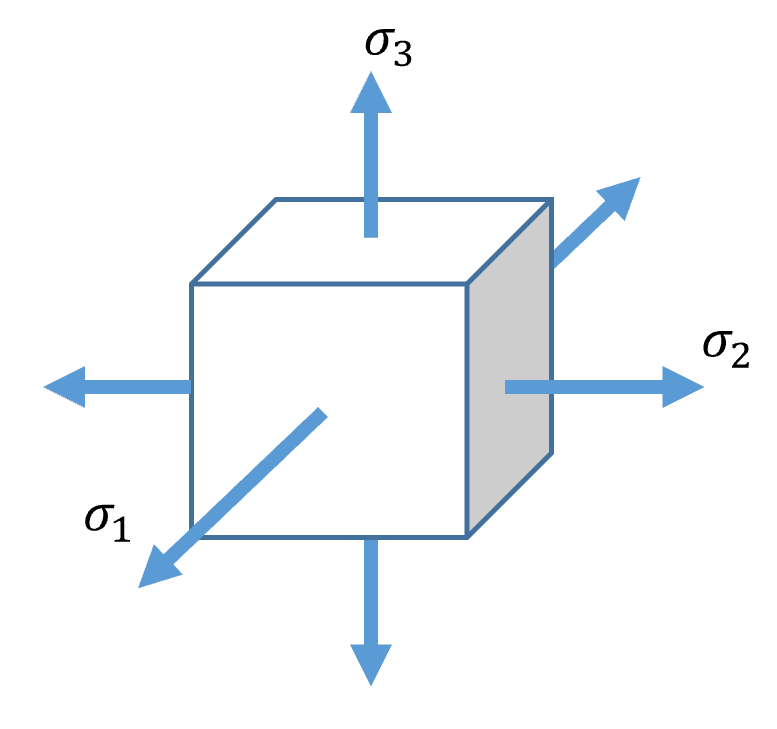
ある要素に生じる垂直応力を図1に示すように考えたとき、例として特徴的な応力状態における応力三軸度ηの値は、

・純せん断状態; σ_{1, 2, 3}=0 ⇒ η =0
・単軸引張状態; σ₁=σ、σ_{2, 3}=0 ⇒ η = 1/3
・等二軸引張状態;σ_{1, 2}=σ、σ₃=0 ⇒ η = 2/3

になることが分かります。
このほかにも試験片形状を変えることで、多様な応力三軸度を再現することが可能です。

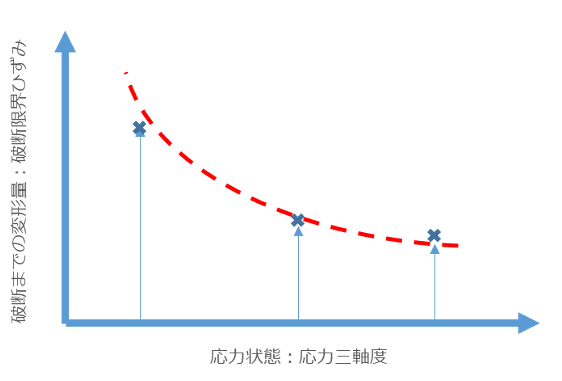
応力三軸度を変えることで材料の破断限界ひずみが変化することが知られており、例えば、図2に示すような破断限界ひずみと応力三軸度の関係が得られます。この関係を定式化し、CAE上で破断の閾値として用いることができます。

試験片の評価部に発生する応力はCAEから、ひずみはデジタル画像相関法(DIC)によって測定することで評価を行います。
デジタル画像相関法についてはこちらをご参照下さい。

サンプル仕様

定型の試験片形状はなく、自動車分野では工夫を凝らした様々な形状が提案されています。ご希望の応力三軸度が再現できるようにCAEを用いて試験片形状の検討から承ります。

評価事例1;アルミニウム合金材の破壊限界ひずみ評価

アルミニウム合金材(A6061-T6 板厚3mm)について評価し、得られた破断限界ひずみの応力三軸度依存性を図3に示します。図3には、各応力三軸度を再現するための試験片評価部におけるひずみ分布のコンター図も一緒に示しています。定式化した曲線のフィッティングには、以下の式(4)を用いています。

　ε^p=α∙exp(−β∙η)・・・(4)

ここで、
ε^p :破断限界ひずみ(相当塑性ひずみで表します)
η :応力三軸度
α, β:フィッティング定数

このほか、ご指定の式でのフィッティングも対応可能です。

破断限界ひずみの応力三軸度依存性

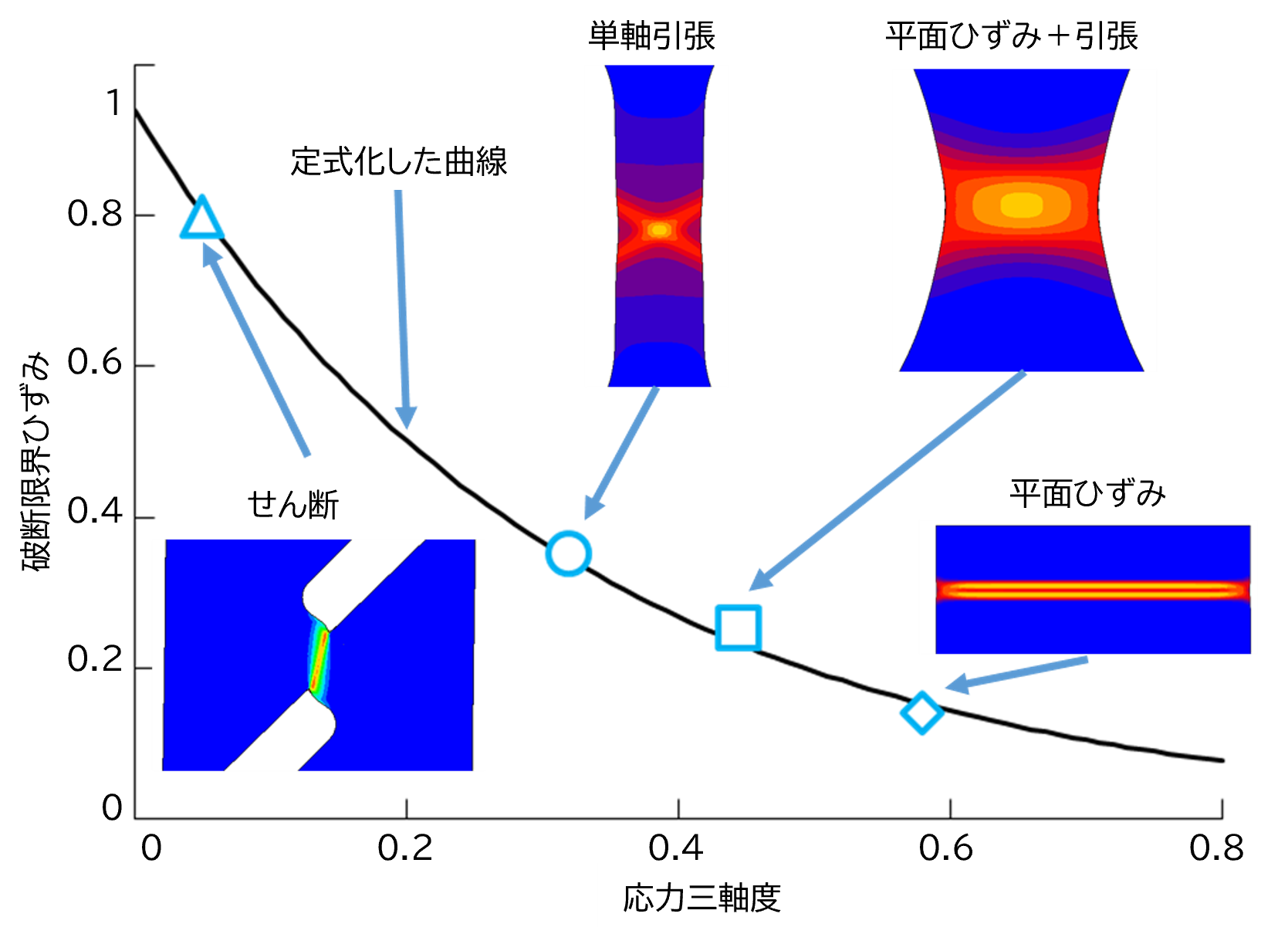
　　　　　　　　(各応力三軸度を再現するための試験片評価部におけるひずみ分布のコンター図)

評価事例2;GISSMOパラメータ導出および簡易モデルによる破断限界評価

GISSMOとは、Generalized Incremental Stress-State dependent damage MOdelの略であり、応力三軸度とロードパラメータを考慮し、応力状態の詳細を反映した破断の発生を予測するダメージモデルです。LS-DYNAに標準搭載されており、破断限界評価のために利用しやすいモデルです。

せん断から等二軸変形までを想定した複数の試験片形状で試験を実施し、それを模擬したCAE(数値解析)の結果を基にモデルの表現に必要なパラメータを決定します

材料試験とCAEによる破壊限界曲面の推定

本事例では自動車用高強度鋼板980MPa材で評価した例を示します。
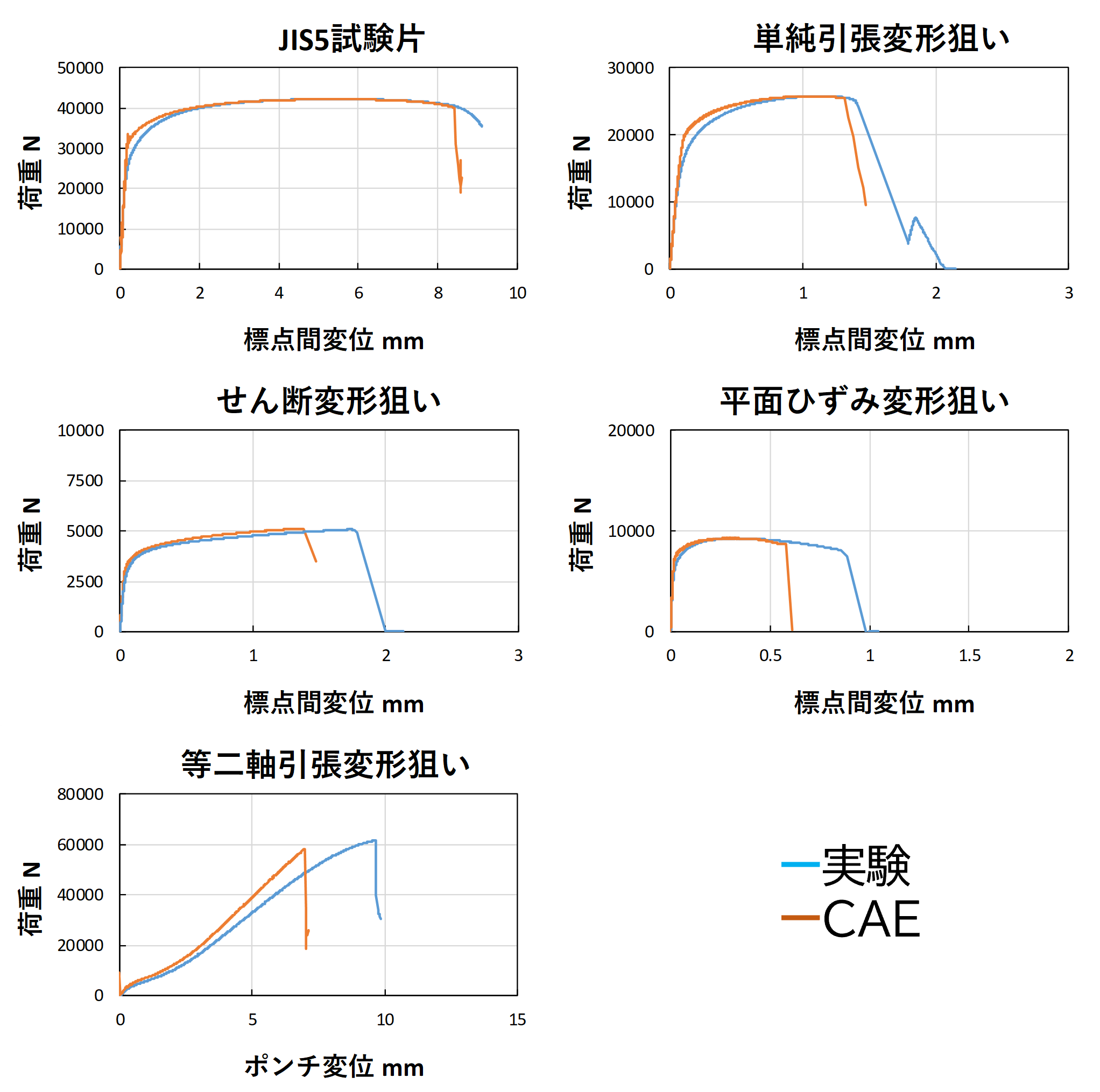
応力状態の異なる5形状の試験片について材料試験とCAEによる再現解析を行った結果を図4に示します。図中の縦軸は発生した荷重、横軸は評点間変位の関係を示しています。

この実験データから破断のタイミングを決定します(青色線図)。
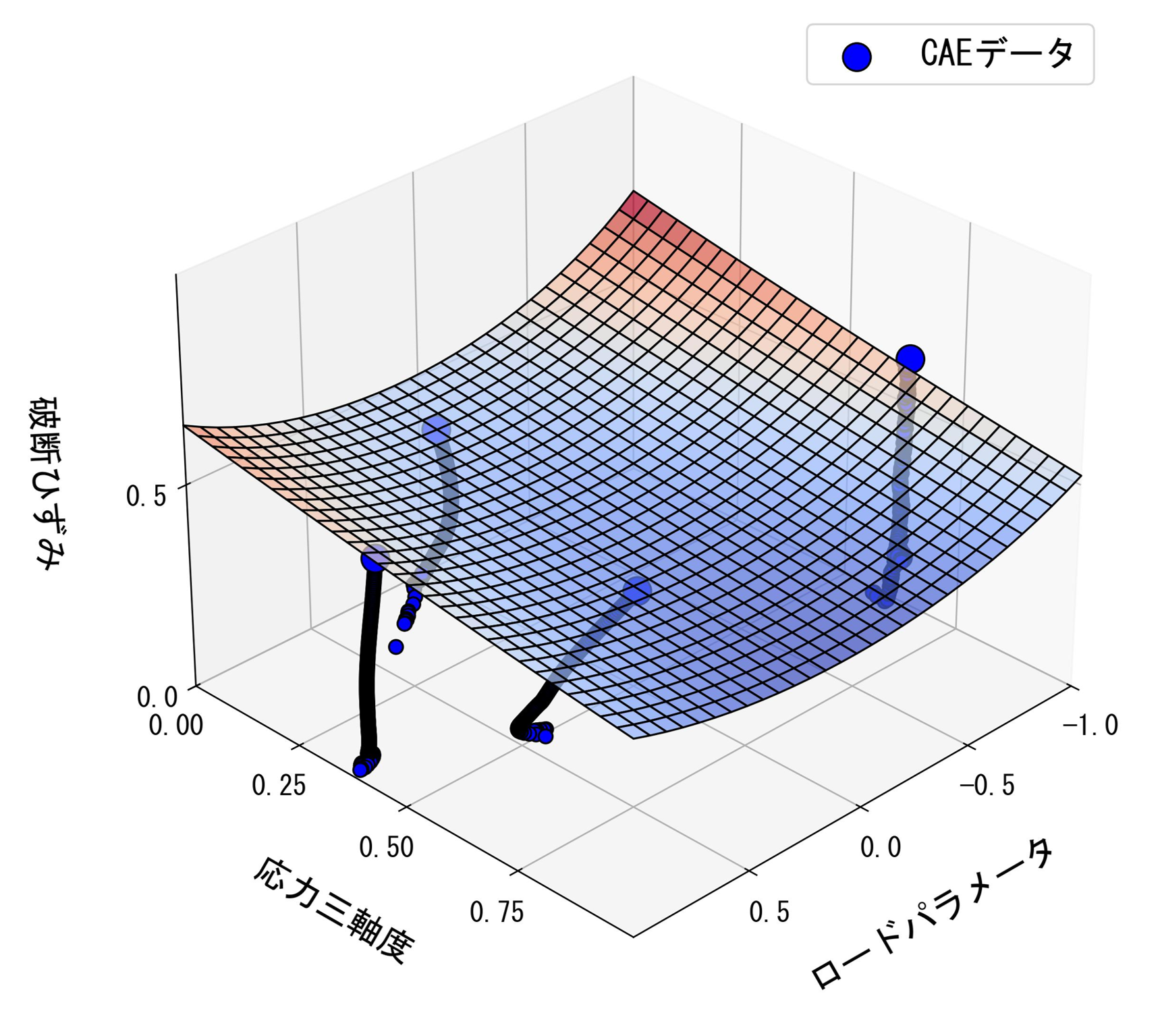
次に、CAEの解析結果(赤色線図)から応力三軸度、ひずみ、およびロードパラメータを求め、Modified Mohr-Coulomb(MMC)モデル用のパラメータを決定します。得られた破断曲面を図5に示します。

・実験とCAE結果の比較(荷重と変位の関係)

・実験データと推定された破断曲面

模擬自動車部品の破断CAEと実験との対比

前述の素材を使用してピラー部材を模擬したハット試験体の三点曲げ試験および同様のCAEを実施しました。図6に三点曲げ試験の模式図を示します。

ハット試験体の中央には穴加工を施し、破断の発生位置を限定しています。
GISSMOモデルと一般的な単軸引張試験の破断ひずみから破断閾値を決定した簡易モデルを比較しました。

・ハット部材の三点曲げ模式図

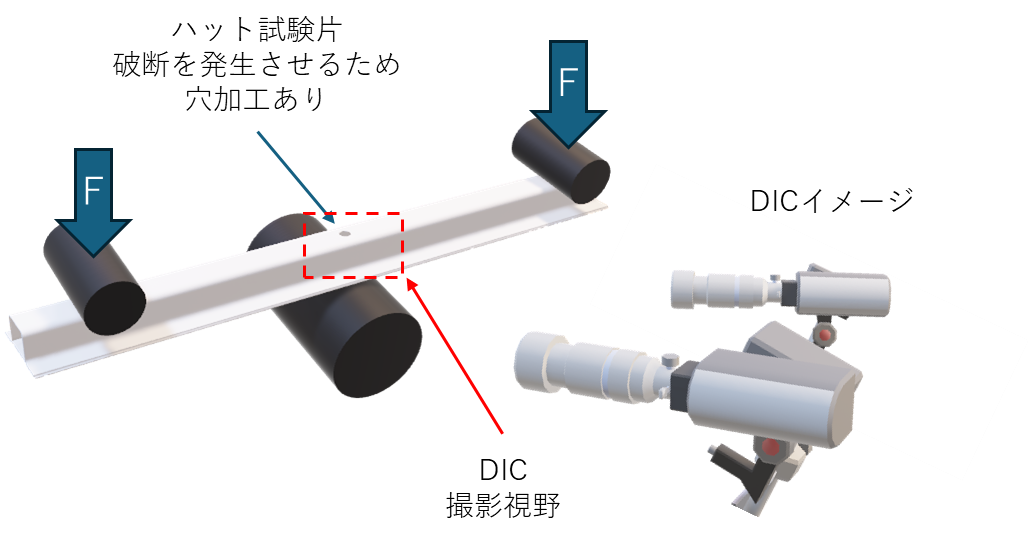
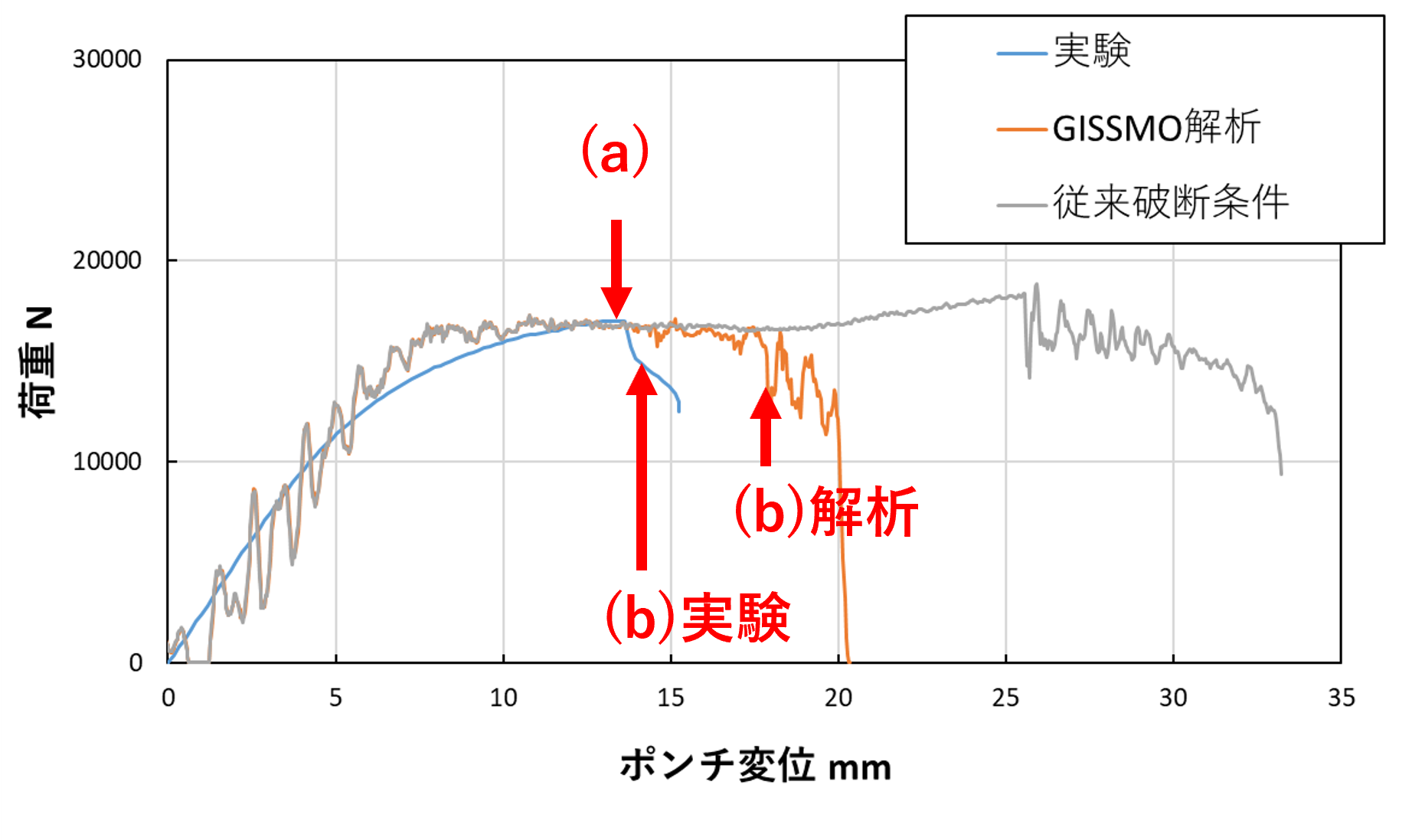
図7に三点曲げ試験時の荷重とポンチ変位の関係、図8にデジタル画像相関法(DIC)とCAEによって求めたひずみ分布状況を示します。
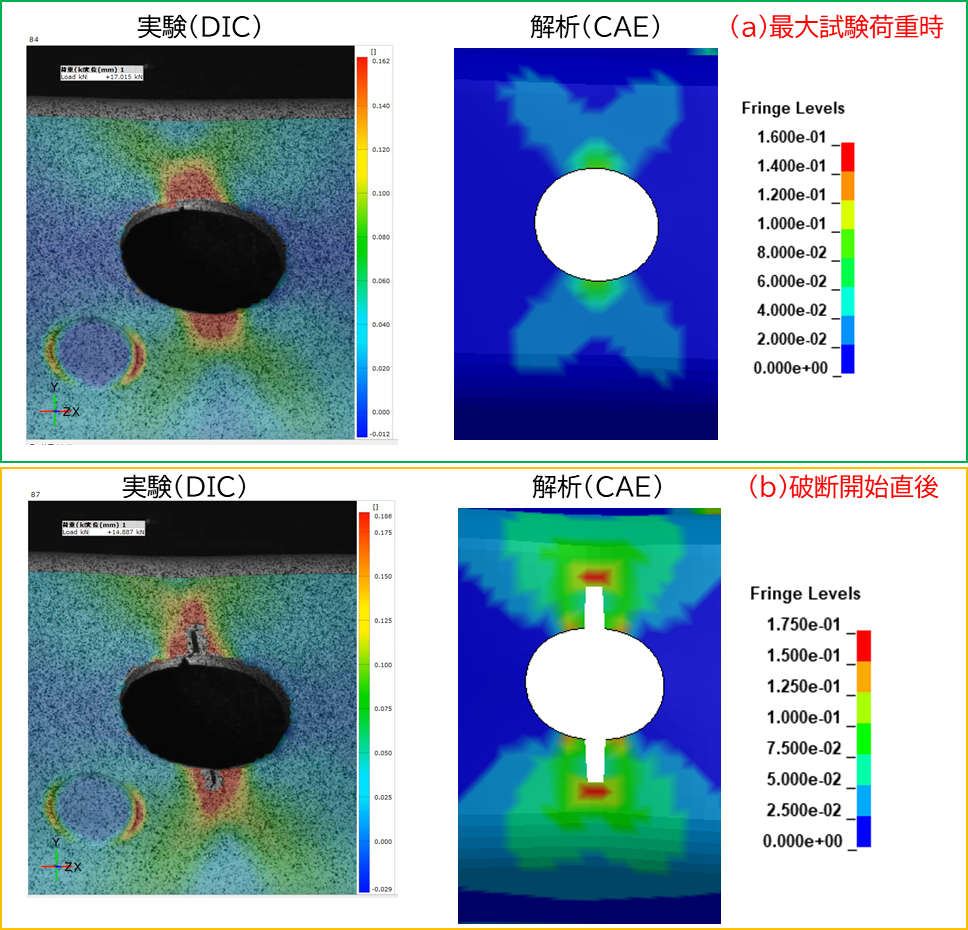
図7の(a)が最大荷重時、 (b)が実験、解析それぞれの破断開始直後を示しており、図8に示すひずみ分布の(a)、(b)と対応しています。
従来破断条件に対し、GISSMOダメージモデルの方が、より実験結果を再現できる結果となりました。
デジタル画像相関法(DIC)によって得られた結果は、CAEの検証用などにご利用いただけます。引張試験機や疲労試験機、成形試験機を用いて対応いたします。

・三点曲げ試験時の荷重と変位の関係

・実験(DIC)と解析(CAE)のひずみ分布状況引

試験から材料カードの作成までを一貫して対応します

当社では、実験とCAEを組み合わせ、さまざまなモデルのパラメータ同定を一貫して実行することが可能です。また、CAEに入力しやすい形式(LS-DYNA用の材料カードなど)での提供にも対応いたします。

装置仕様

引張試験機や疲労試験機、成形試験機を用いて対応致します。