示差熱-熱重量同時分析(TG-DTA)
TG:Thermogravimetry
DTA:Differential Thermal Analysis
示差熱-熱重量同時分析(TG-DTA)とは
示差熱-熱重量同時分析(TG-DTA )では、温度プログラム(昇温速度制御)によって試料温度を変化させ、試料の化学・物理変化により生じる重量変化、温度変化を測定します。測定雰囲気(キャリアガス)として、不活性ガス(Ar,N2)、酸化性ガス(乾燥空気)、還元性ガス(4%H2)に加え、水蒸気導入を選択することができ、試料の相転移温度(固相→固相、固体→液体、液体→気体)や、各種雰囲気における試料の反応性、熱安定性の評価ができます。さらに、速度論的解析から活性化エネルギーを算出することも可能です。
示差熱-熱重量同時分析装置(TG-DTA)
装置仕様
| 装置 | NETZSCH社製 TG-DTA SE型 | |
| 測定温度範囲 | 室温~1500°C(JIS R型の場合) 500~1600°C(JIS B型の場合) |
|
| 測定雰囲気 | Ar、N2、乾燥空気、4%H2、水蒸気導入 | |
| 試料 | 試料量 | 最大1g *試料容器質量含む |
| 試料容器 | アルミニウム、白金、 アルミナ、窒化ホウ素 | |
| 試料形状 | Φ5.0mm×5.1mm | |
示差熱-熱重量同時分析(TG-DTA)の原理
1)TG: Thermogravimetry (熱重量測定)
重量変化が起こると、メインビームが傾きます。その動きを元に戻すようにコイルに流す
電流を制御します。流した電流は重量変化に対応しているので、電流の変動を重量変化として出力します。
2)DTA: differential thermal analysis (示差熱分析)
試料ホルダーに設けられた熱電対により、試料・基準物質の測温を行います。検出された温度差をDAT信号として出力します。
※基準物質・・・測定温度範囲に吸発熱のない物質
(空容器・αアルミナ板など)
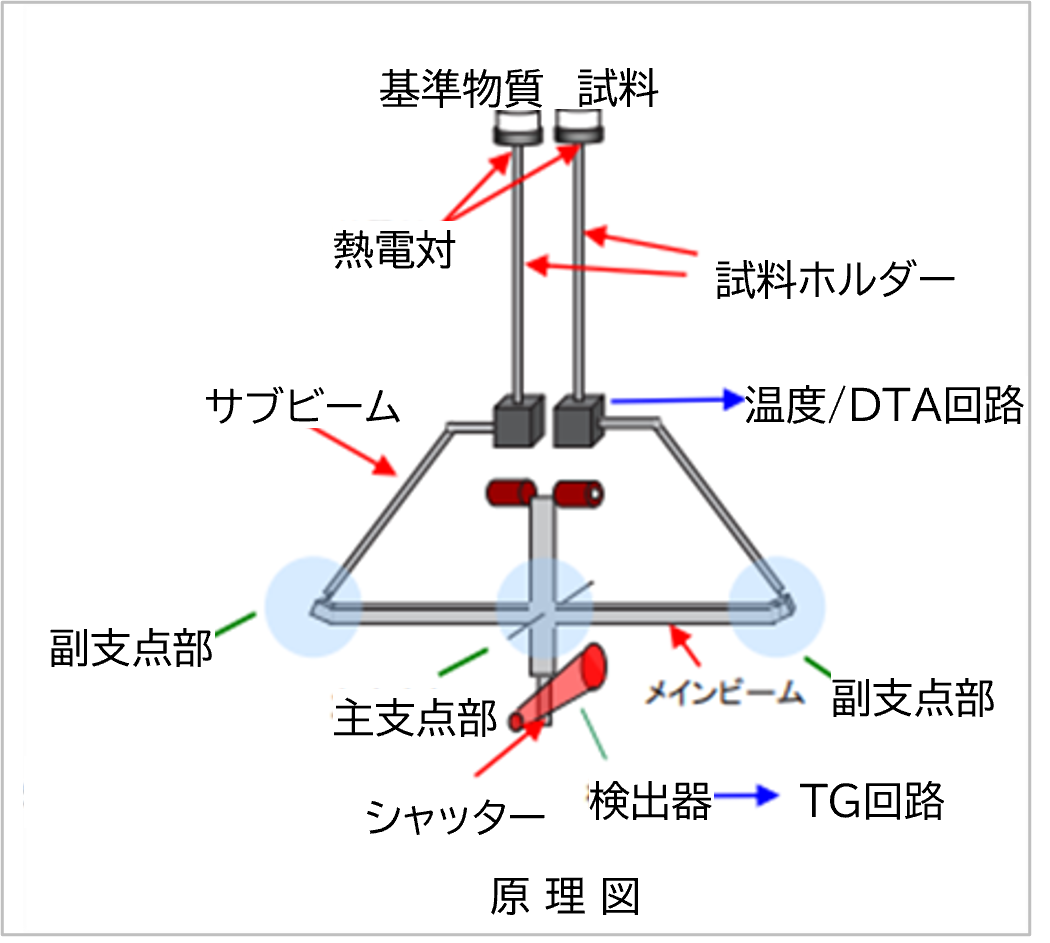
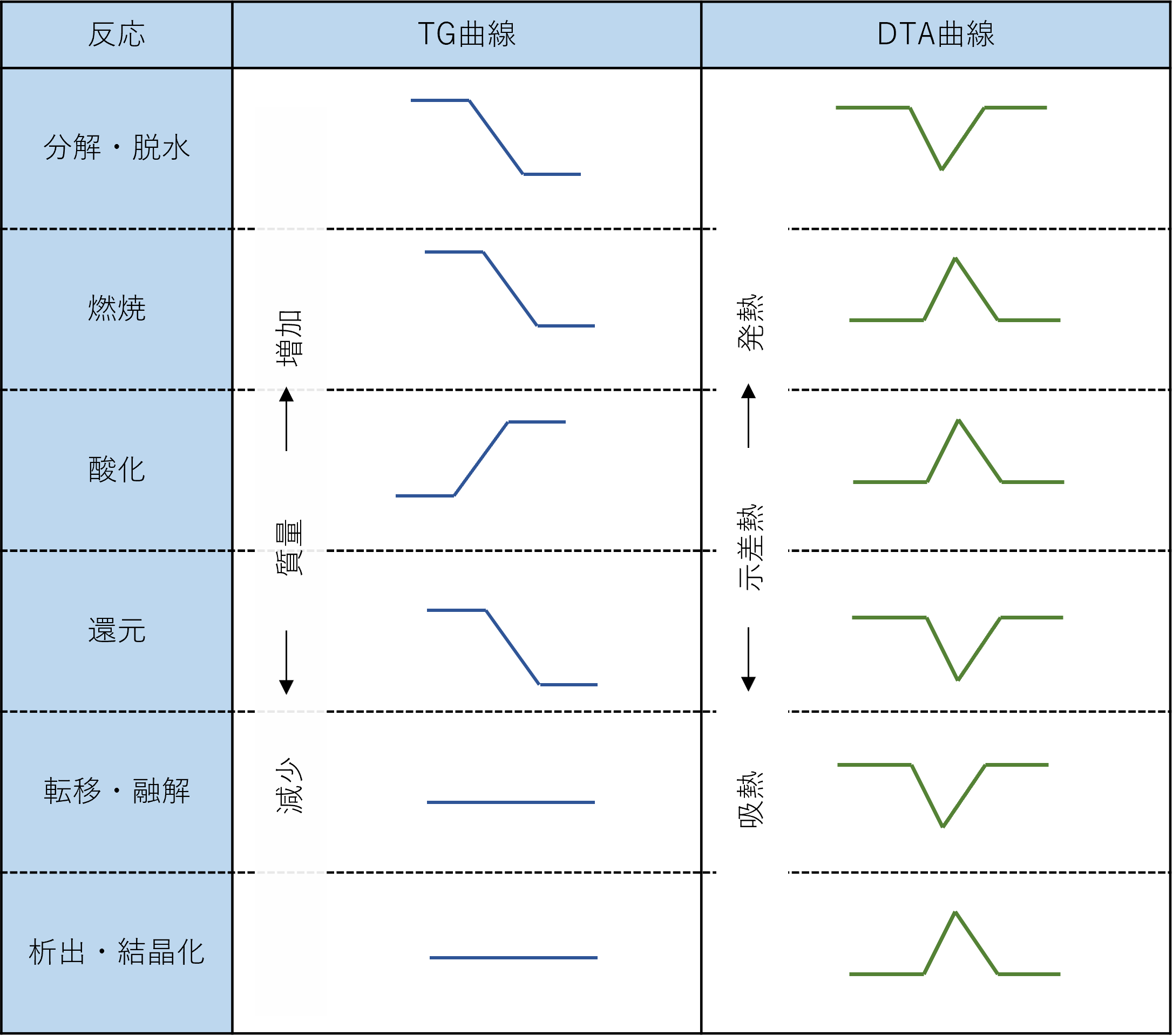
TGとDTAの挙動から、試料内で起こった反応を推察
示差熱-熱重量同時分析(TG-DTA)の事例
事例1; 金属のDTA
- 純パラジウムの融点測定をDTAで行いました。
雰 囲 気:Ar
試料形状:2mm×2mm×1mm
温度範囲 : 1400°C~1600°C (昇温速度:10°C/分)
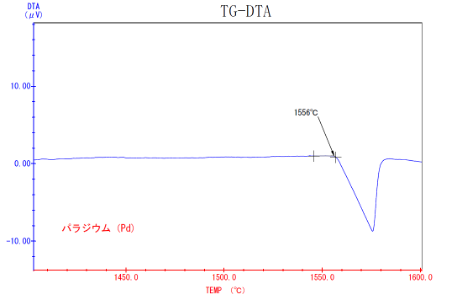
- 純パラジウムの融点(文献値)1555°Cに対して、測定結果は1556°Cでした。
- 公差±3°Cで管理を実施しており、測定結果は公差内の結果でした。
事例2; 水蒸気導入TG-DTA測定
水蒸気発生ユニットとの接続により、水蒸気圧制御を行った窒素や空気(Wetガス)を導入しながら最高1000°Cまでの測定も可能です。
装置仕様(水蒸気導入測定時)
| 項目 | 仕様 |
|---|---|
| 測定下限温度 | 導入水蒸気圧により異なりますので、ご相談下さい |
| 測定上限温度 | 1000°C |
| 測定雰囲気 | 窒素(N2)、空気(Air)、各水蒸気圧制御ガス |
| ガス流量 | 250ml/min 内訳:Dry+Wetガス200ml/min+保護ガス(Dryガス)50ml/min |
| 水蒸気圧制御範囲 | 0~45kPa(導入水蒸気圧や測定開始温度により制約があります) 例)200°C等温時→最大30kPaの水蒸気圧制御ガス導入可能 10kPaの水蒸気圧制御ガス導入→測定開始温度は75°C以上 |
| 水蒸気圧安定性 | ±0.5kPa |
| 昇温速度 | 通常10°C/min(上限20°C/min) |
| 容器 | アルミニウム(上限温度500°C)、白金、アルミナ |
| 試料サイズ | 最大5mmΦ(通常5~10mg程度) |
水蒸気圧制御原理
導入ガス1気圧(101.3kPa)中の水蒸気の分圧を制御することで、測定ガスの湿度調整を行います。
例:導入水蒸気圧
0 kPa=Dryガスのみ ⇒ 0(kPa)/101.3(kPa)=0 (%)
20 kPa=Wetガス+Dryガス ⇒ 20(kPa)/101.3(kPa)=19.7(%)
※1気圧(101.3kPa)を基準とした相対水蒸気圧
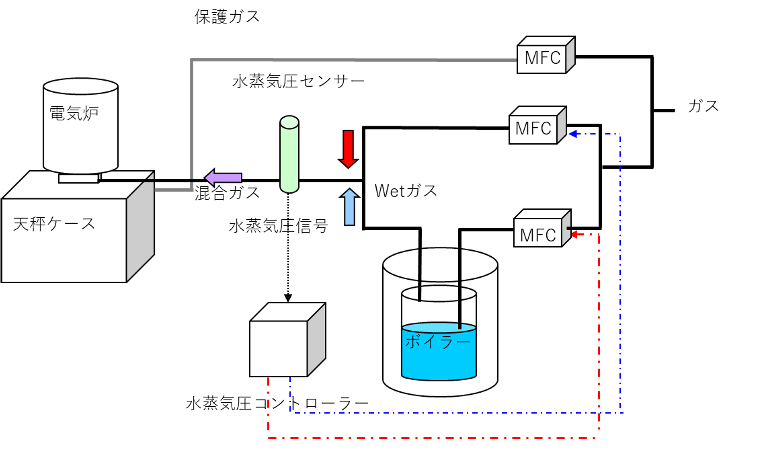
水蒸気圧制御原理
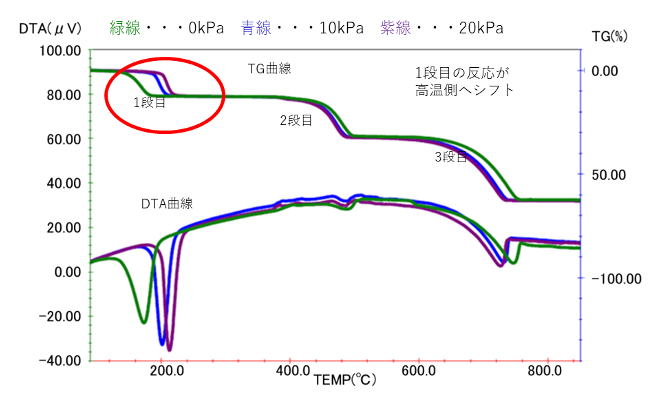
シュウ酸カルシウム水和物の熱分解評価
同じ温度プログラムで、水蒸気圧を変えてTG-DTA測定を行い、熱分解温度の差を確認しました。
シュウ酸カルシウム水和物の熱分解反応を化学式で表すと
1段目 CaC2O4・H2O → CaC2O4 + H2O↑
2段目 CaC2O4 → CaCO3 + CO↑
3段目 CaCO3 → CaO +CO2↑
となります。
水蒸気を導入することで1段目の反応が高温側にシフトし、シュウ酸カルシウム水和物中の水分の脱離が遅くなることが分かりました。
事例3; TG/DTAによるPMMA熱分解の活性化エネルギー算出
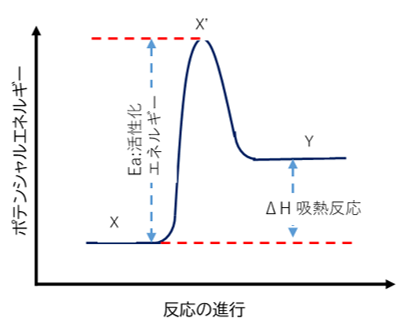
- X(出発物質)が、Y(生成物)に変化する反応において、反応の出発物質の基底状態から遷移状態(X’)に励起するのに必要なエネルギーである。活性化エネルギーの壁を超えるエネルギー(熱)を受け取る事で、X→Yの反応が進行する。
- 活性化エネルギーは、物質の分子構造とその熱に対する挙動との関連を表現してくれる値であり、燃焼性や耐熱性評価の重要な指標となります。
TG-DTAによる活性化エネルギー算出事例
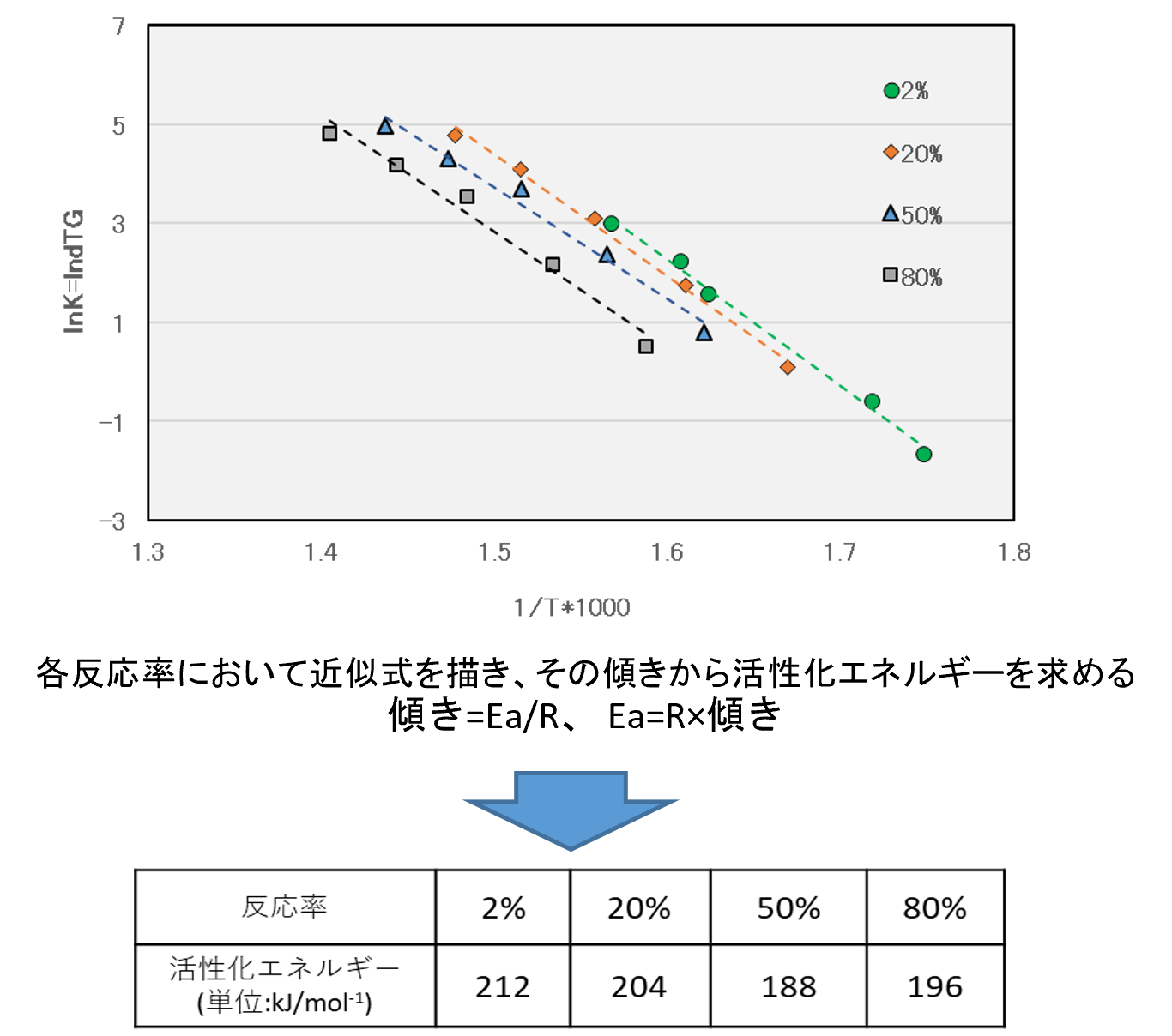
ポリメタクリル酸メチル(PMMA)粉末を5水準の昇温速度で測定し、
小沢-Friedman 法(ISO11358-3)に従い、熱分解の活性化エネルギーを算出しました。
(小沢-Friedman 法)
アレニウス式( k = Ae-Ea/RT )を使用 両辺の対数(自然対数)をとると
Ln(k) =-Ea/RT+ln(A) →logek =-(Ea/R)*(1/T) + ln(A)
K: 反応速度定数 T:絶対温度 R:気体定数 Ea:活性化エネルギーA: 頻度因子(定数)
1/Tを横軸にln(k)(k=dTG%)を縦軸にとってグラフを描き得られた直線の傾きは-E/Rに相当する事から活性化エネルギーを算出
T:絶対温度 R:気体定数 Ea:活性化エネルギーA: 頻度因子(定数)
※小沢-Friedman法適用範囲
・反応が単一であること。
・アレニウスプロットの直線になる部分で活性化エネルギー算出が可能。
・算出された活性化エネルギーは、同一条件(測定条件・測定機器・解析方法)で測定・解析したもののみ比較評価可能。
このグラフはTG-DTA測定における、各昇温速度の各反応率における反応速度定数(k=dTG)の自然対数を縦軸、それら反応率の温度の逆数を横軸にプロットしたグラフです。傾きに気体定数を乗じる事で、活性化エネルギーを算出します。
※ 高分子の熱分解時の活性化エネルギーは、同じ種類場合、分子量、分子量分布、雰囲気等の影響を受けます。
公的規格
- JIS K 0129 熱分析通則
- JIS H 7151 アモルファス金属の結晶化温度測定方法 (DSC,DTA)
- JIS K 6226 ゴム-熱重量測定による加硫ゴム及び未加硫ゴム組成の求め方(TG)
- JIS K 7120 プラスチックの熱重量測定方法
- ISO 11358 Thermogravimetry (TG) of polymers
参考技術資料
関連する技術
- 熱膨張(TD)
- 熱伝導率測定
- 剛体振り子型物性試験
- 熱特性評価
- 熱線法熱伝導率測定
- 比熱容量
- 熱伝達測定
- 断熱法<比熱容量>
- 示差走査熱量計(DSC)
- 熱機械分析法(TMA)
- フラッシュ法を用いた熱拡散率・熱伝導率測定
- 温度傾斜法<熱伝導率/界面熱抵抗>
- 灰溶融性測定
- ヤング率、剛性率、ポアソン比、内部摩擦測定
関連する分類
熱特性評価
- 熱膨張(TD)
- 熱伝導率測定
- 剛体振り子型物性試験
- 示差熱-熱重量同時分析(TG-DTA)
- 熱特性評価
- 熱線法熱伝導率測定
- 比熱容量
- 熱伝達測定
- 断熱法<比熱容量>
- 示差走査熱量計(DSC)
- 熱機械分析法(TMA)
- フラッシュ法を用いた熱拡散率・熱伝導率測定
- 温度傾斜法<熱伝導率/界面熱抵抗>
- 灰溶融性測定
- ヤング率、剛性率、ポアソン比、内部摩擦測定
粉体・焼結体特性
- ゼータ電位・粒子径測定
- 石炭及びコークスのハードグローブ粉砕性指数(HGI)測定
- 密度測定
- マルチテスターによる粉体物性評価(流動性・噴流性)
- 粉体材料の比表面積・細孔分布測定
- 粉体・焼結体特性
- 粒子径・粒度分布測定
磁気特性評価
燃料・危険物の特性評価