熱力学計算

熱力学計算とは

鉄鋼材料、非鉄金属の熱処理条件検討において、実験とともに熱力学計算を併用することは、現象のメカニズム解明、効率化による経費削減等の効果が期待されます。当社では、材料の熱平衡を計算で求めるCALPHAD法(CALculation of PHAse Diagrams)を用いて、状態図をはじめとする各熱力学データを導出し、金属材料組織制御に関するプロセス課題解決、新材料開発を支援します。

熱力学計算の概要について説明します。

熱力学計算とは、calphad法と呼ばれ平衡状態図を計算で求める方法として、1970年代頃から普及しはじめました。

計算フローは、まず実験や第一原理計算より決定された状態図作成に必要なギブス自由エネルギー関数を集めたデータベースを用意します。そして、対象となる材料のギブス自由エネルギー関数の最小化計算を温度、組成を入力値として、ソフトウェアで計算します。その結果として、状態図、平衡相の量などのデータ出力が可能です。

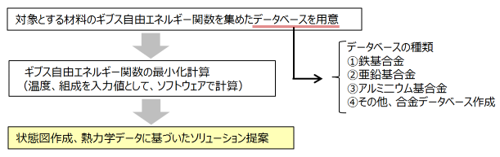
ここで、計算精度のキーとなるのが、データベースになります。計算データベースの種類は、主なもので現在3つあります。1つ目は鉄基合金で22元素に対応しており、多元素系の計算が可能です。2つ目は亜鉛基合金で、こちらは、Zn,Al,Mg,Si,Feの元素系に対応してます。3つ目は、アルミ基合金です。こちらは、Al-Cu-Fe-Mg-Mn-Ni-Siなどの元素系で計算可能です。その他、適宜必要な合金系でのデータベースを作成することも可能です。

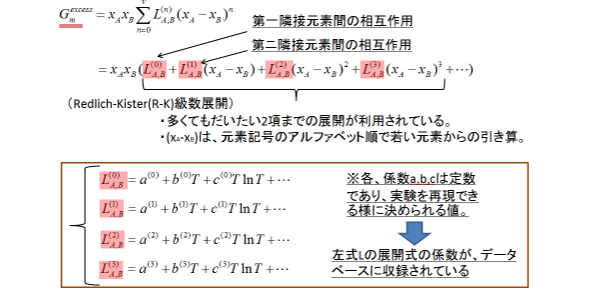
データベースに収録してあるギブス自由エネルギーは、材料を構成している各元素の純物質の項の数値、また元素間の相互作用エネルギーの項の数値になります。特に、多元素系では、各元素間の相互作用エネルギー値がそろっているかどうかで、計算精度に影響します。

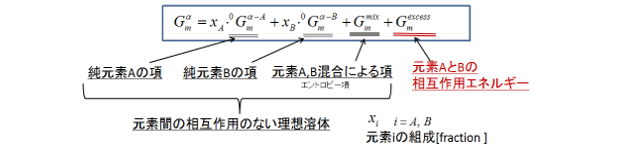
図2は、2元素系の溶体相の正則溶体近似モデルによるギブス自由エネルギーの定式化例です。多元素で構成される相、化合物のエネルギーの形態についても、元素数を拡張することで基本的には同様の形式で表せます。

熱力学計算解析ツール

• メーカー 型 株式会社 計算熱力学研究所 CatCalc SE
• 計算方法 CALPHAD法
• 計算モデル 正則溶体近似による固溶体モデル、副格子モデル。
  シャイル(Scheil)モデル(凝固計算)
• データベース 鉄基合金、亜鉛基合金、アルミ基合金 など

熱力学計算の適用分野

• 多元素系の合金の状態図作成
• 熱処理による析出相の評価
• 固溶限の推定・融点予測
• 溶融金属の凝固過程における晶出相評価、凝固組織予測

熱力学計算の事例

事例1;多元素系の状態図作成による金属材料組織予測

• 対象:2相ステンレスSUS821L1 (組成:Fe-0.01C-0.5Si-3Mn-21Cr-2Ni-0.1Mo-0.17N-1Cu)
• 目的:オーステナイトとフェライトの相比率が等しくなる熱処理条件(温度・組成)を得る

2相ステンレスの多元素系状態図作成例について説明します。4元素系以上の多元系の状態図では、注目組成を横軸にとり、他の元素は固定して、縦軸に温度をとる形で表現されることが多いです。図3は、2相ステンレスの計算状態図で、横軸Cr濃度、縦軸は温度です。他の組成は固定してます。2相ステンレスなので、オーステナイトとフェライトの混合領域が広がっていることが確認できます。この様に状態図は、相の領域、融点や変態温度などを一目で確認できます。

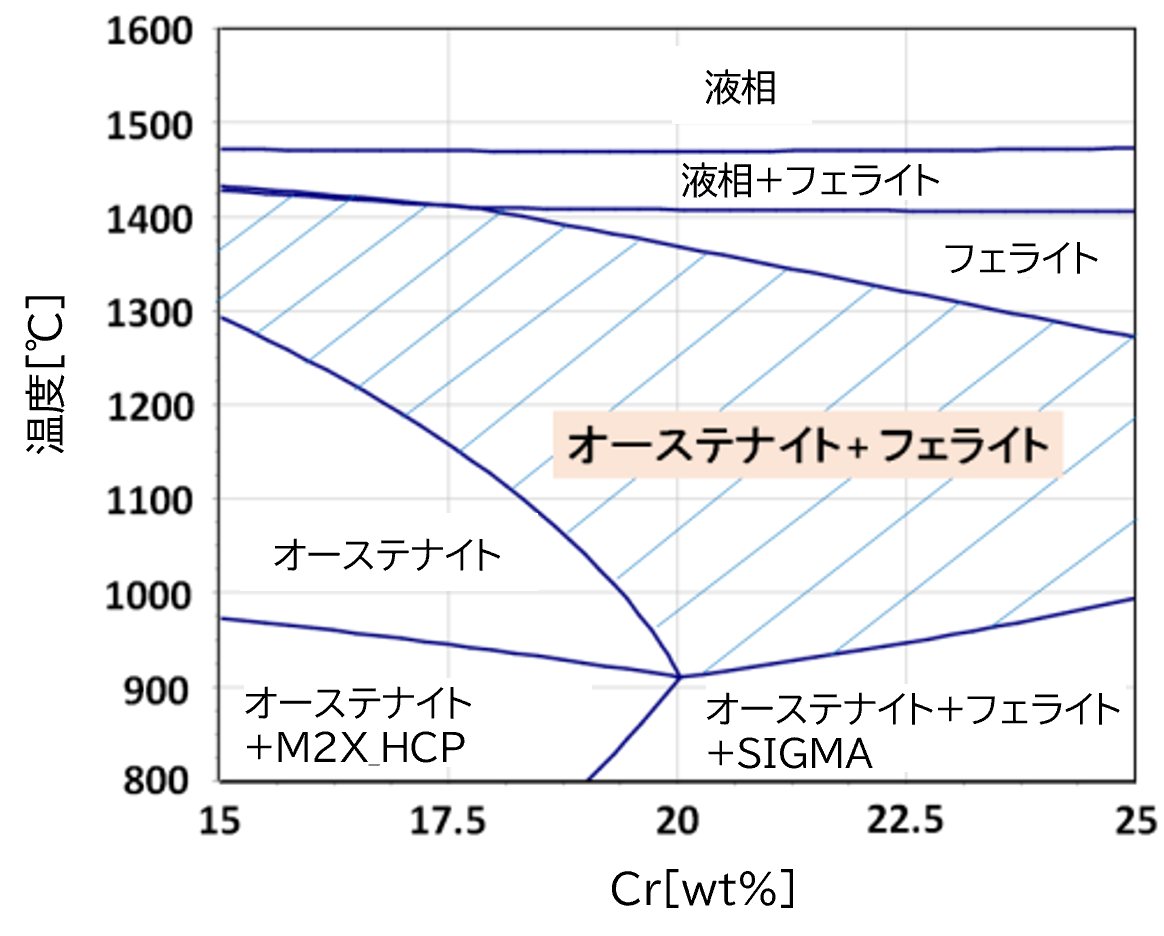
しかし、図3から相の量がどの程度出ているのかという情報を得ることはできません。2元系の状態図では手計算(てこの原理)で相の量を計算可能ですが、多元素系になると、状態図上から読み取ることはできません。そこで、各相の自由エネルギーから相の量をソフトウェアを用いて計算出力致します。

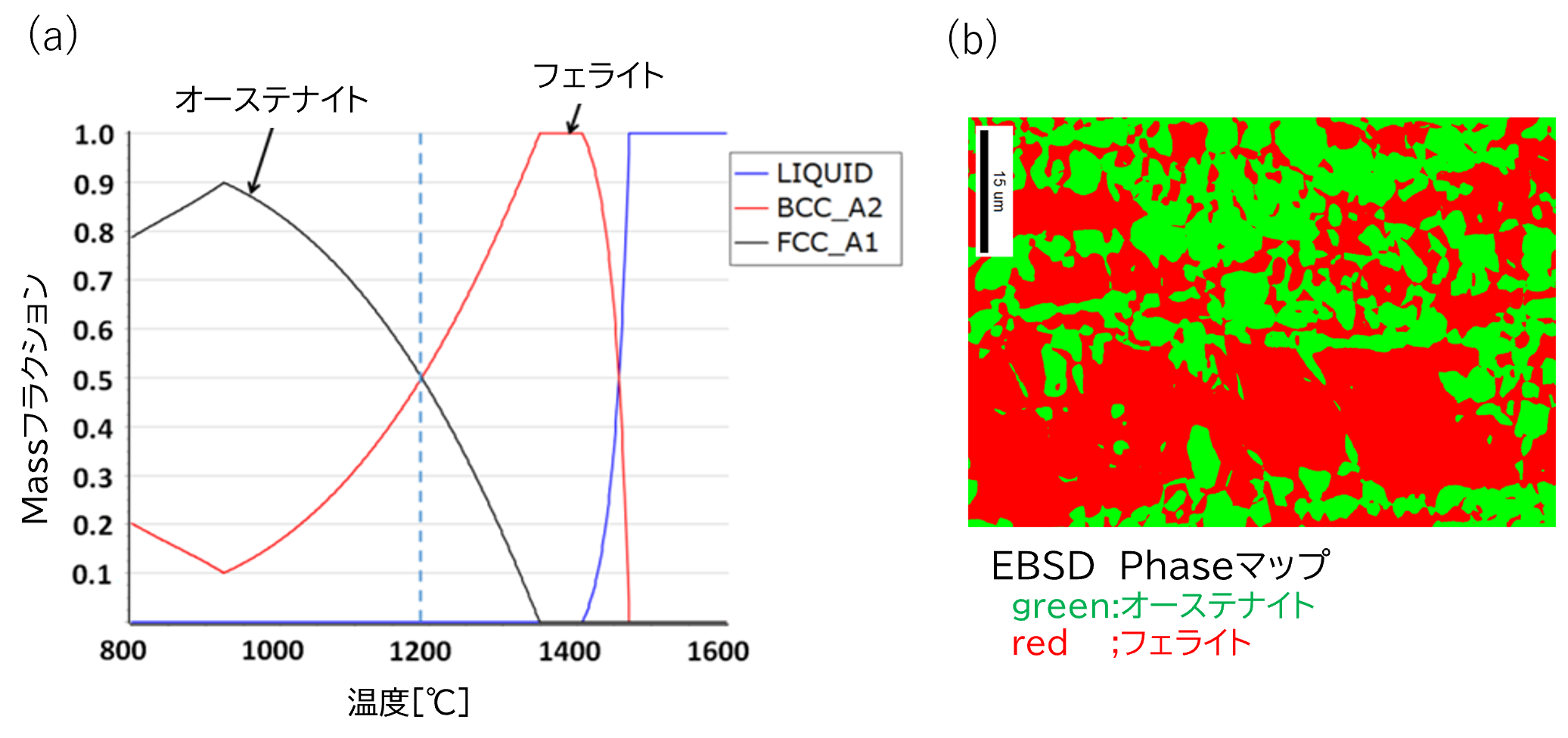
図4(a)は、図3の状態図のCrを21%で固定したラインでの各相の量変化を示したグラフです。横軸は温度で縦軸は相の量です。1200°C付近でオーステナイトとフェライトが同じ量程度出ていることが分かります。図4(b)は、計算で実施したのと同じ2相ステンレスのEBSDのPhaseマップの結果です。緑色の部分がオーステナイト、赤の部分がフェライトで、ほぼ1:1に存在していることが分かります。

計算を用いることで、金属組織の形成条件(温度、組成)の情報を得ることが可能です。また、相変態の時間依存については、平衡状態図に加えてTTT線図、CCT線図等を用いて検討します。

事例2; 鋼中炭化物の評価例

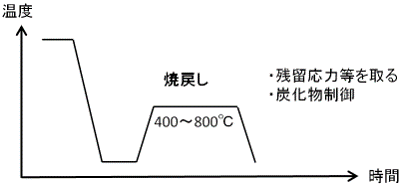
鋼中炭化物の量的な評価例について、焼戻し工程に着目します。焼戻しとは、焼入れ後に、残留応力をとったり、炭化物の制御をするために、再度400~800°Cで熱処理する工程です。焼戻し工程での炭化物の種類、量についての評価について説明します。

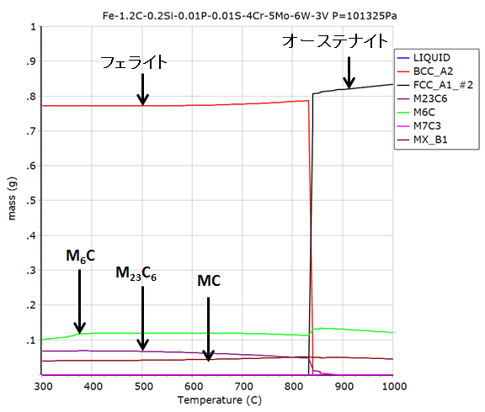
• 対象:鋼速度工具鋼  SKH53 (組成:Fe-1.2C-0.2Si-0.01P-0.01S-4Cr-5Mo-6W-3V)
• 目的:鋼速度工具鋼  SKH53の熱処理中の炭化物量のデータ出力

鋼中炭化物量の評価例についてご説明します。図7は、高速度工具中の炭化物量の温度依存性の平衡計算結果です。横軸は温度で、縦軸は相の量マスフラクションです。300°C~800°Cの間でフェライト中にこれら炭化物が存在していることが分かります。この結果は、焼戻し工程での炭化物種類、量の予測などに使われ、最適な熱処理条件(温度・組成)の検討に役立てられています。

平衡計算では、十分時間が経った時の組織を予測することは可能ですが、時間に依存した途中の状態を知ることはできません。焼戻しは、炭化物を温度と時間で制御するので、時間依存性も合わせて考察します。例題の高速度工具鋼の場合、Cr, Mo, W, Vが比較的多く添加されています。よって、表1の様に各元素に応じた炭化物が反応時間とともに形成されます。反応初期では、M₃C(セメンタイト)が生成され、時間経過とともに、M₇C₃,  M₂Cなどの中間生成物を経て、M₂₃C₆, M₆C, MCなどの炭化物が生成して平衡状態に収束していきます。熱処理時間が短い場合は、M₃C(セメンタイト), M₇C₃,  M2C の様な準安定状態と呼ばれる平衡状態の次に安定な状態で組織が決まります。

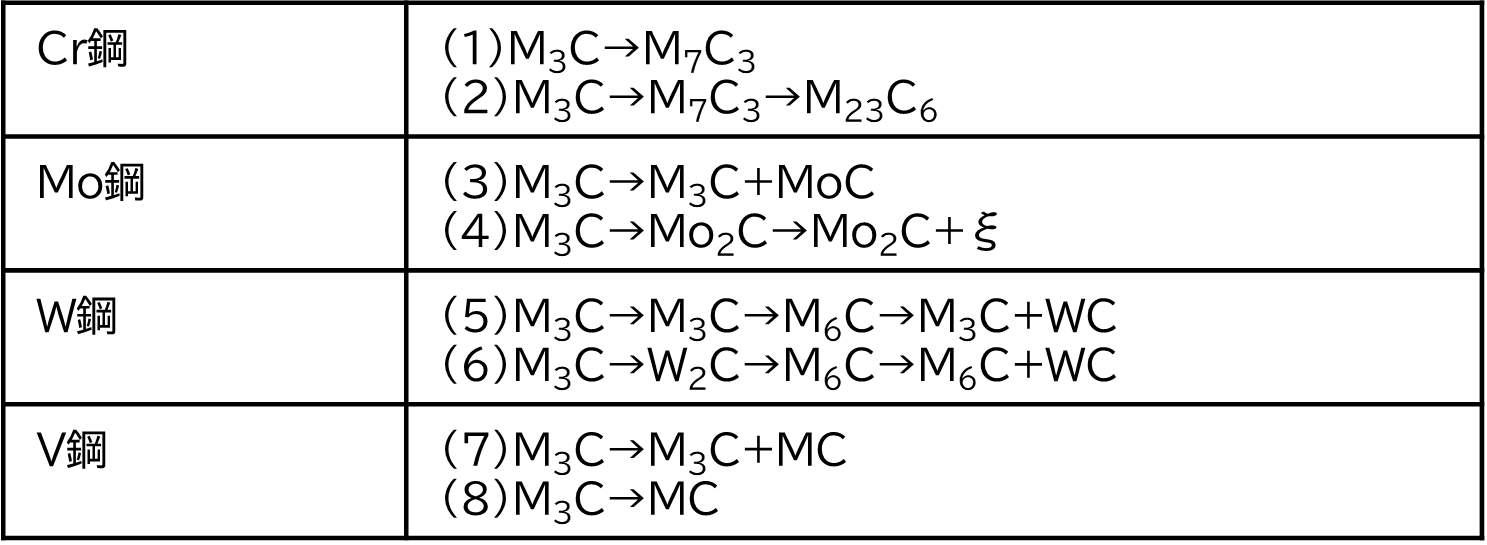
図8は、高速度工具中の炭化物量の温度依存性の準安定状態の計算例です。横軸は温度で、縦軸は相の量マスフラクションです。充分時間が経った状態で現れる析出物(M₆C, M₂₃C₆  , MC等)を平衡計算の対象から外すことで、準安定状態を計算します。平衡状態に至る前の段階で一時的に生成される炭化物の検討を行う際に有効です。

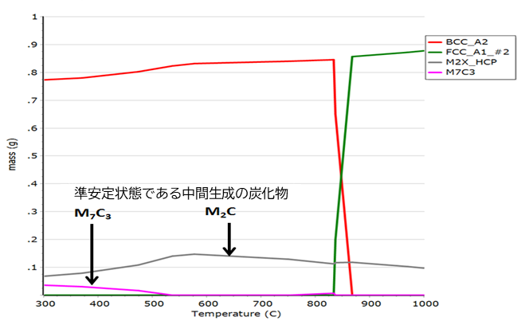
更に、図9は、高速度工具鋼SKHの析出物の時間依存性を計算した例です。M₃C, M₇C₃が初期に析出して、その後、M₂₃C₆, M₆C, MCなどの平衡組織になることが分かります。これは、表1の傾向とも一致しています。熱力学計算をベースとして、速度論的な情報を組み合わせて、プロセスのソリューションを志向します。

事例3; 凝固組織予測シミュレーション例

• 対象:ジュラルミン (組成:Al-4Cu-0.7Mg)
• 目的:ジュラルミンの凝固組織予測

事例3は、シャイル凝固計算による凝固組織予測シミュレーション例の紹介です。シャイルの凝固計算につきましては、『液相側の拡散は十分早く、固体側は拡散を無視』※という仮定のもとの計算手法になります。冷却中(徐冷)の固相中の濃度分布を比較的良く表しており、凝固計算には広く使われています。温度をΔT毎下げながら平衡計算を実施するが、前ステップの相分配、組成分配の情報を引き継いで次の計算されるため、平衡状態図どおりの平衡凝固と比較して、非平衡現象に近いところも再現可能であり、凝固終端での凝固偏析を評価することも可能です。徐冷付近の冷却過程であれば適用範囲と考えられます。

※シャイルモデルでは、『液相側の拡散は十分早く、固体側は拡散を無視』という仮定のもと、温度ステップに分けて晶出量の推移を見るモデルですが、修正シャイルモデルは、固相中の主元素の拡散は無いとしますが、格子間元素のように小さなものは固相内で拡散して平衡になると仮定します。これは逆拡散(Back-Diffusion)モデルとも言います。格子間元素(炭素など)が存在している場合は、固体中で拡散しているとした修正シャイルモデルを使用して凝固を評価します。

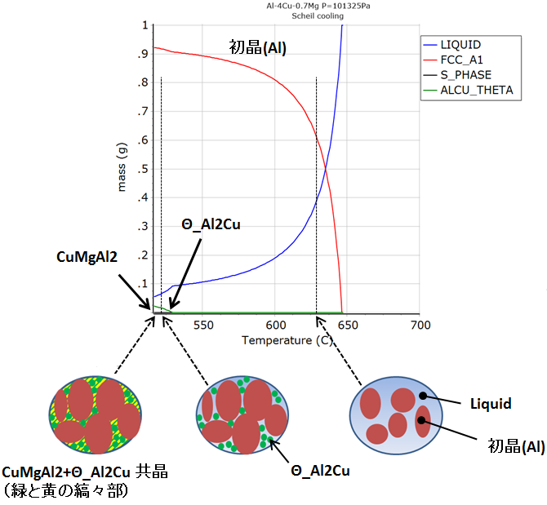
事例3の計算対象の合金は、Al-Cu-Mg系ジュラルミンです。この系では、Al2Cuなどの相を晶出させて強化する材料です。図10は、Cu4%固定で、横軸Mg、縦軸温度の計算状態図です。本計算では、点線の矢印の方向に700°Cの液相からの凝固組織を予測致します。

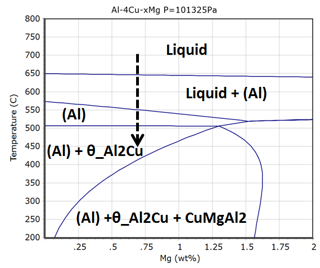
図11は、凝固シミュレーションの結果です。横軸温度で縦軸は、相の量です。青ラインの液相が温度低下とともに減少して、初晶のAlが出て、その後、Al2Cuが出て、凝固間際にAl2CuとCuMgAl2の共晶が出ることがわかります。このグラフから凝固組織を予測したのが、グラフ下の絵です。液相から初晶Alが出た後、Al2Cuが出て、凝固間際にAl2CuとCuMgAl2の共晶が出る組織が推測されます。

参考技術資料

• FTM-2006  熱力学計算による金属材料組織への応用